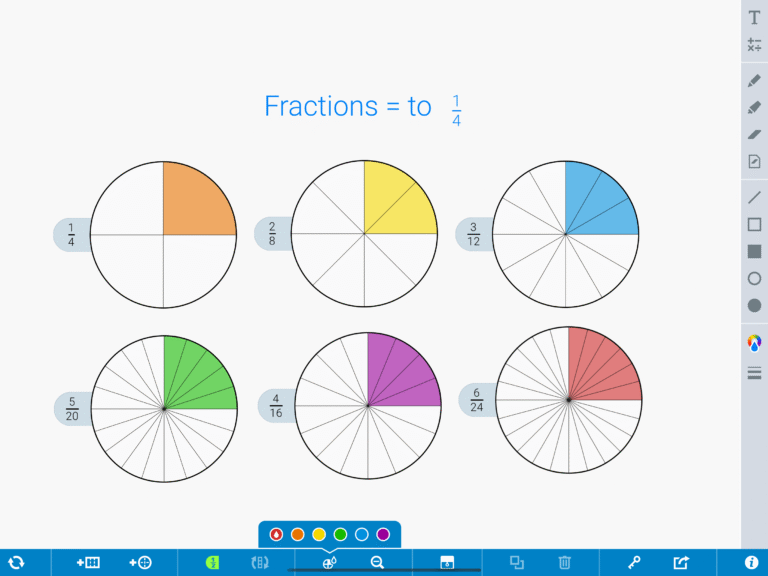
✅ Compará numeradores y denominadores: igualá denominadores o usá decimales para descubrir rápido qué fracción es mayor.
Para saber qué fracción es mayor entre dos o más, es fundamental entender cómo comparar fracciones a través de métodos sencillos y efectivos, como la comparación de denominadores, la conversión a fracciones comunes o la conversión a números decimales.
Exploraremos detalladamente las distintas técnicas para identificar cuál fracción es mayor, incluyendo ejemplos prácticos, consejos para evitar errores comunes y herramientas que te ayudarán a dominar esta habilidad matemática de manera clara y rápida.
Métodos para comparar fracciones
Existen varios métodos para determinar cuál fracción es mayor:
1. Comparar fracciones con el mismo denominador
Cuando las fracciones tienen el mismo denominador, comparar es muy sencillo: basta con comparar los numeradores.
- Ejemplo: 3/7 y 5/7
- 5/7 es mayor que 3/7 porque 5 > 3.
2. Comparar fracciones con el mismo numerador
Si las fracciones tienen el mismo numerador, gana la fracción que tenga el menor denominador, ya que al dividir el numerador en menos partes, cada parte es más grande.
- Ejemplo: 3/4 y 3/5
- 3/4 es mayor que 3/5 porque 4 < 5, por lo tanto, cada parte es más grande.
3. Igualar denominadores usando el mínimo común denominador (MCD)
Cuando las fracciones tienen distintos denominadores, una forma efectiva de compararlas es encontrar el mínimo común múltiplo (MCM) de los denominadores para igualarlos.
- Calcular el MCM de los denominadores.
- Convertir cada fracción a una equivalente con denominador igual al MCM.
- Comparar los numeradores resultantes.
Ejemplo: Comparar 2/3 y 3/5
- MCM de 3 y 5 es 15.
- Convertir: 2/3 = 10/15 y 3/5 = 9/15.
- Comparar numeradores: 10 > 9, por lo que 2/3 es mayor que 3/5.
4. Convertir a números decimales
Otra manera simple es convertir las fracciones a números decimales dividiendo el numerador por el denominador y luego comparar los resultados.
- Ejemplo: 7/8 y 5/6
- 7 ÷ 8 = 0,875 y 5 ÷ 6 ≈ 0,833
- Por lo tanto, 7/8 es mayor que 5/6.
Consejos para comparar fracciones
- Usar el método que te resulte más sencillo: para fracciones con denominadores iguales, compara numeradores; para numeradores iguales, compara denominadores.
- Practicar con ejemplos variados: esto te ayudará a identificar rápidamente cuál fracción es mayor sin cálculos complejos.
- Evitar errores en el cálculo del MCM: es clave para convertir fracciones correctamente.
- Verificar con decimales: si tienes dudas, convertir a decimal es una comprobación rápida y segura.
Métodos prácticos para comparar fracciones de manera sencilla y rápida
Comparar fracciones puede parecer una tarea complicada a primera vista, pero con algunos métodos prácticos y bien aplicados, se vuelve un proceso rápido y eficiente. A continuación, te presentamos las técnicas más utilizadas para determinar cuál fracción es mayor entre dos o más, así como ejemplos concretos y consejos para que puedas aplicarlas sin errores.
1. Método del denominador común
El primer paso para comparar fracciones es convertirlas a un denominador común. Esto facilita la comparación porque sólo tenés que mirar el numerador para saber cuál es mayor.
- Ejemplo: Comparar 3/4 y 5/6
- Buscamos el mínimo común denominador (MCD) de 4 y 6, que es 12.
- Convertimos las fracciones: 3/4 = 9/12 y 5/6 = 10/12.
- Comparando los numeradores, 9 < 10, por lo tanto, 5/6 es mayor que 3/4.
Ventajas:
- Fácil de entender y aplicar.
- Ideal cuando los denominadores no son muy grandes.
2. Método de la cruz o producto cruzado
Este método es especialmente útil cuando querés comparar dos fracciones sin necesidad de encontrar un denominador común. Se multiplican cruzadamente los numeradores y denominadores, y se comparan los resultados.
- Ejemplo: Comparar 2/5 y 3/7
- Multiplicamos cruzado: 2 × 7 = 14 y 3 × 5 = 15.
- Como 15 > 14, entonces 3/7 es mayor que 2/5.
Consejo práctico:
Este método es muy útil para hacer comparaciones rápidas en exámenes o cuando no querés perder tiempo con denominadores grandes.
3. Convertir fracciones a números decimales
Otra manera intuitiva de comparar fracciones es convertirlas a decimales dividiendo el numerador por el denominador. Después, simplemente comparás los números decimales obtenidos.
- Ejemplo: Comparar 7/8 y 5/6
- 7 ÷ 8 = 0.875
- 5 ÷ 6 ≈ 0.8333
- Por lo tanto, 7/8 es mayor que 5/6.
Precaución:
Este método puede presentar problemas con números decimales muy largos o periódicos, por lo que es recomendable usarlo cuando se busca una comparación aproximada.
Tabla comparativa de métodos
| Método | Ventajas | Desventajas | Uso recomendado |
|---|---|---|---|
| Denominador común | Claridad en la comparación, fácil para denominadores pequeños | Poco práctico con denominadores grandes | Cuando los denominadores son manejables |
| Producto cruzado | Rápido, sin necesidad de hallar denominadores comunes | Solo para dos fracciones a la vez | Comparar dos fracciones rápidamente |
| Conversión a decimal | Intuitivo y fácil de aplicar | Puede perder precisión con decimales periódicos | Comparaciones aproximadas y rápidas |
¿Cuándo usar cada método?
- Si trabajás con múltiples fracciones, preferí el denominador común para evitar errores.
- Para comparaciones rápidas de dos fracciones, el producto cruzado es tu mejor aliado.
- Si buscás algo intuitivo y sencillo, convertí a decimal, pero tené en cuenta la precisión.
Recordá que practicar con diferentes tipos de fracciones te ayudará a dominar estos métodos y elegir el que mejor se adapte a cada situación.
Preguntas frecuentes
¿Qué es una fracción?
Una fracción representa una parte de un todo y se expresa con un numerador y un denominador.
¿Cómo comparo fracciones con igual denominador?
La fracción con el numerador más grande es la mayor.
¿Cómo comparo fracciones con distinto denominador?
Se igualan los denominadores usando el mínimo común múltiplo y luego se comparan los numeradores.
¿Puedo convertir las fracciones a decimales para compararlas?
Sí, convertir fracciones a decimales es una forma rápida de ver cuál es mayor.
¿Qué pasa si las fracciones son impropias?
Se aplican las mismas reglas; también se pueden convertir a números mixtos para facilitar la comparación.
| Paso | Descripción | Ejemplo |
|---|---|---|
| 1 | Identificar denominadores | Comparar 3/4 y 2/3 → Denominadores 4 y 3 |
| 2 | Encontrar Mínimo Común Múltiplo (MCM) | MCM de 4 y 3 es 12 |
| 3 | Convertir fracciones | 3/4 = 9/12 y 2/3 = 8/12 |
| 4 | Comparar numeradores | 9 > 8 → 3/4 es mayor |
| 5 | Alternativa: convertir a decimales | 3/4 = 0,75 y 2/3 ≈ 0,6667 |
Dejá tus comentarios abajo y no te pierdas otros artículos de nuestra web sobre matemáticas y educación que pueden interesarte.